你有莫得想过妈妈 调教，在当代物理的规模里，还有一个见解是咱们无法绕昔日的？就像物理学的“恶势力”相通，它不单是是一个单纯的数学器具，而是鼓励了物理学的和解和发展，这个见解便是张量。
张量的玄妙和复杂让好多东说念主视为畏途，但它亦然当代物理学不成或缺的一部分，它匡助咱们更真切地清晰物理天下的实质，张量背后的数学和物理深度更是令东说念主敬畏。
一、张量的发祥：拉伸的真谛，张量便是高维空间中的“拉伸”
张量这个名字源于拉丁词“拉伸”，张量便是高维空间中的“拉伸”这个见解。张量不错看作是一个多维数组，它的每一个维度对应一个物理量，而这些物理量之间的斟酌则由张量的具体形势来默示。
在某种道理上，张量就像是高维数列的一个膨大，它不错在高维空间中花式物理量之间的斟酌， 比如咱们在界说物体的刚性时，可能需要引入一个称为刚度张量的量，它便是通过拉伸界说的。
轻熟女
二、张量的身份：花式物理景色的要道器具
(1)张量的界说，变换坐标时保握物理道理不变
那么，张量是什么呢？通俗来说，张量便是一种在变换坐标时保握物理道理不变的数学对象，张量的界说相比概述，但不错通过以下两个方面来清晰：
第一，张量的变换划定。张量在坐标变换下的变化司法叫作念“变换划定”，它是张量的中枢特征之一， 举例，若是一个物理量在某一坐标系下被默示为一个张量 T，在另一个坐标系下它不错通过一定的变换划定再行默示为一个新的张量T'，但物理景色的实质不会因为坐标系的不同而有所变化。
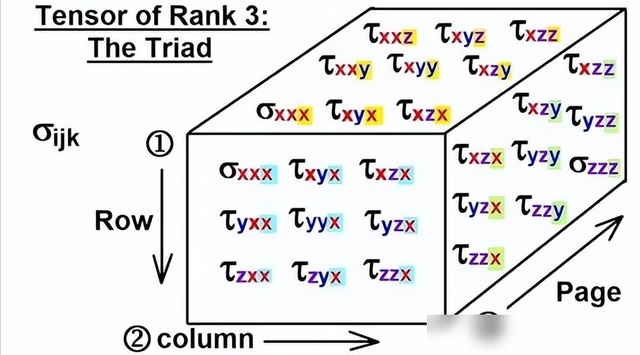
第二，张量的几何默示。每个张量齐有其对应的几何对象，张量的阶数（也称为张量的维度）和张量的维度是两个寥寂的见解，比如零阶张量是标量，一阶张量是向量，二阶张量巧合也称为矩阵，它在三维天下中特别于一个立体，三阶和更高的张量就有点复杂了，需要同期接头到多个维度的变换，触及到好多复杂的诡计。
因此，在试验愚弄中，咱们往往不会触及跨越三阶的张量，大无数物理学家和工程师只需要处理零阶到二阶张量， 比如电场强度是二阶张量，电荷是零阶张量。
(2)张量在物理中何如体现？看这几个例子
①应力张量
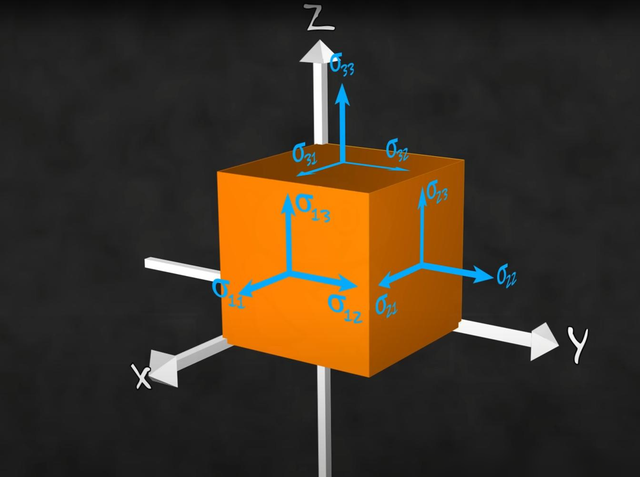
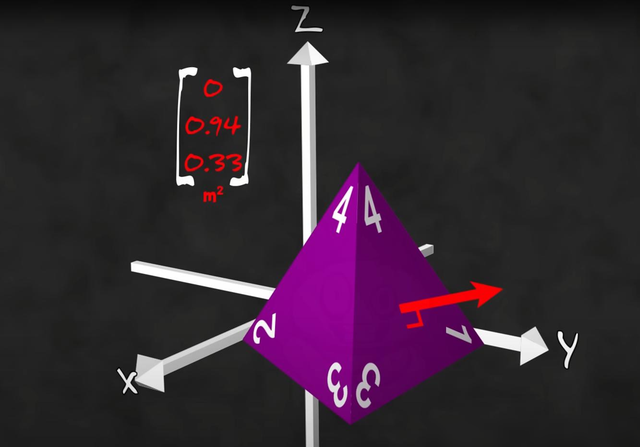
在物理学中妈妈 调教，张量的愚弄相配庸碌， 其中一个攻击的愚弄便是在花式物体在不同方进取受到的力的散播情况，这时，就需要用到一种罕见的张量，称为应力张量。应力张量是一种二阶、三维张量，它花式的是在一个材料里面随心小数上，由外界施加的压力或拉力散播情况。
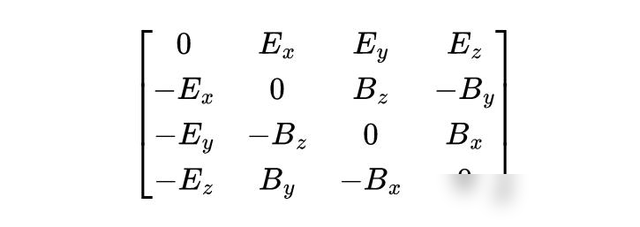
应力张量包含了材料的弹性性质和变形行动等信息，是力学分析中不成或缺的器具。关于一个立方体，咱们不错用一个三维的立方体来默示它的受力情况， 每个面上的箭头默示力的大小和标的，张量的三维性也反应出了物理量的多维性，力不仅不错用三维向量默示，试验上它的影响还可能是多维的，量子物理中粒子的自旋便是一个典型的例子。
②电磁场张量
电磁场张量是花式电磁场的一个攻击器具，它是一个四维的张量，通过它不错快速便捷地诡计出各式电磁场的物理量，如电场强度、磁场强度等。电磁场张量是一个四维张量，它包含了电场和磁场的信息，是花式电磁场的一个攻击器具。
在经典力学中，电场和磁场是两个寥寂的物理量，但在相对论中，它们被和解为一个四维张量，通过电磁场张量，咱们不错更便捷地诡计电磁场的各式物理量，如电场强度、磁场强度等， 在量子物理中，电磁场张量也有攻击的愚弄，如粒子的互相作用和放射等。
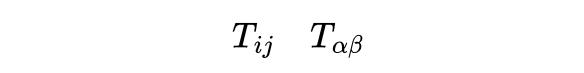
电磁场张量的全称是法拉第张量，四个重量分袂为： 电场强度E的重量Ex，Ey，Ez和磁感应强度B的重量Bx，By，Bz。在四维时空中，法拉第张量不错用一个 4×4的反对称张量来默示，这个形势就像左侧这个表格相通，四维电磁场张量的重量在坐标变换下是这么变化的 ，如法拉第张量的重量Fμν在洛伦兹变换下的变化司法便是：F'μν = LμLνFαβ，这个性质便是张量的界说。
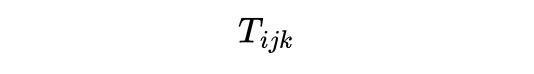
③实在的向量VS伪向量，区别在这里
在物理学中，往往将矢量称为“实在的向量”，而将物理道理上和实在的向量雷同的量称为“伪向量”，伪向量和实在的向量的主要区别在于坐标系的改革何如影响它们的物理道理。
当咱们将一个实在的向量从一个坐标系滚动到另一个坐标系时，它的物理道理是不变的，比如速率便是一个实在向量，速率的界说便是： v = dx/dt，dx是物体在时候t到t+dt之间的位移，其标的和大小是不变的。而伪向量在坐标系之间的滚动时，可能会出现反向变换，导致其物理道剃头生变化。
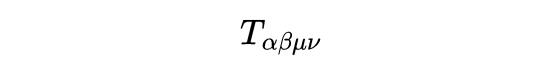
举例，在经典力学中， 物体的角动量便是一个伪向量，在静止坐标系下物体的角动量是L = r × p， 物体以等速率平片时，角动量的值并不会发生变化，但其标的会因坐标系的不同而不同；而速率行为一个实在的向量， 则不会因坐标系的滚动而改革其大小和标的，以向量形势默示为 v = (vx，vy，vz)，vx，vy，vz的标志齐是不变的。
三、张量的魔力：探索时空和物资景色的器具
01、时空的神奇：四维速率（4-Velocity）
在当代物理学中，咱们频频会遭逢一些看似概述的见解，但它们试验上是匡助咱们清晰天地的一把钥匙。其中，四维速率（4-Velocity）便是这么一个攻击的器具。
四维速率是一个四维向量，它花式的是物体在四维时空中的速率变化。与咱们平方生存中所熟知的三维速率不同，四维速率接头了时候这一维度，因此它愈加全面地反应了物体在时空中的畅通现象。在广义相对论中，四维速率是花式物体目田下跌、轨说念畅通等景色的攻击器具。
02、物资的玄机：电磁场张量
电磁场张量是花式电磁场的一个攻击器具，它在当代物理学中饰演着攻击脚色，匡助咱们清晰电磁景色的实质。电磁场张量是一个四维张量，它包含了电场和磁场的信息，通过电磁场张量，咱们不错快速便捷地诡计出各式电磁场的物理量，如电场强度、磁场强度等。
在经典力学中，电场和磁场是两个寥寂的物理量，它们分袂用电场强度和磁感应强度来默示。而在相对论中，它们被和解为一个四维张量，称为法拉第张量，它包含了电场和磁场的信息，通过电磁场张量，咱们不错更便捷地诡计电场和磁场的各式物理量。
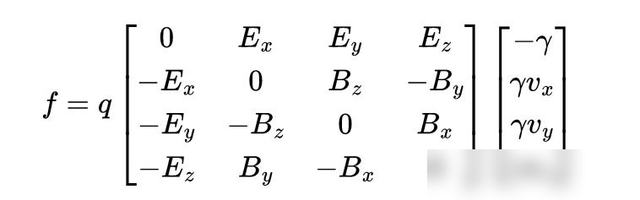
03、追念：张量的实质是“各维度间的斟酌”
张量不仅是一种数学器具，更是一种真切清晰物理景色的路线，它通过花式不同物理量之间的斟酌，匡助咱们揭示了物理景色背后的玄机。需要防范的是， 张量的重量在坐标变换下会变化，但其物理道理不会随之改革，这便是张量的实质。
［四］感悟张量的和解性：从复杂到通俗的轨范化念念路
在张量的学习中，咱们迟缓刚劲到物理的司法是不错“和解”的，从多个不同的景色中索求出疏导的实质，这亦然张量的魔力场地，它让咱们在复杂的数学中找到和解的司法。
跟着当代物理的不停发展，咱们可能会发现更多的高阶张量的愚弄， 比如在量子物理中，张量不错用来默示粒子的量子态和量子态之间的斟酌，在天地学中，张量不错用来花式天地的演化和结构等，这些愚弄齐为咱们提供了新的念念路和方法。
张量的学习并不像假想中那么复杂，借助可视化本领，咱们不错更好地清晰张量的见解和性质，比如在处理高阶张量时，咱们不错使用高维数组的可视化本领，以利于咱们清晰高阶张量的性质，这里的高维数组可视化便是一个很好的例子，它不错匡助咱们更好地清晰高阶张量的性质和愚弄。
在材料科学中，张量也不错行为分析材料变形和应力的广宽器具， 通过对张量的分析，咱们不错究诘新材料的性能偏执在不同条款下的愚弄，举例，究诘材料在高温、高压等极点条款下的性能，还不错探讨何如通过优化张量的性质，进步材料的性能和可靠性。
张量的愚弄相配庸碌，它不仅不错用于科罚复杂的物理问题，也不错用于花式和分析各式当然景色。跟着对张量的真切清晰，咱们将大略更好地清晰和愚弄这个攻击的见解妈妈 调教，为物理学的和解和发展作念出更大的孝顺。